学习函数式编程的一个记录，分成两篇，上篇主要介绍函数式编程的三个主要特征（纯函数、一等公民、不可变性）以及函数编码（高阶函数、柯里化、函数组合），在不可变性中，研究可持久化的数据结构和 Proxy 代理代替可持久化。

Foreword

在之前的开发过程中只是简单了解过函数式编程，随着对于前端内容的学习，发现函数式思想渗透前端生态。React、Redux、RxJS 等都背靠函数式编程思想，我认为有必要认真学习主流思想。最开始接触 JS 时，没有考虑过编程范式，一直采用的是命令式编程和面向对象编程，后来才知道有函数式编程，在区分命令式编程和函数式编程之前，这里我想提及书中一句话：

“遗憾的是，在我们所生存的现实世界中，OOP 往往主宰了很多开发者的思维。当你手里只有一把锤子的时候，你看什么都像钉子。这就好像一个人一生只见过一种世界观、也只能理解这一种世界观，由于他不听、不看、不思考任何其它的世界观，于是只能被迫地狂热痴迷这唯一的一种世界观，这就谈不上信仰与否，而是被世界观所奴役了。“

刚入行，思维停留在过去使用 C++进行解决问题的阶段，一步一步去告诉计算机如何执行程序，多数时候都是直接原生 JS，后来了解到数组方法，慢慢会用这些东西：reduce、map、filter、find、some、every 等等，只是觉得很方便，现在看来数组方法确实是非常重要的函数式编程工具。

根据维基百科的对函数式编程的定义：

函数式编程是一种编程范式，它将电脑运算视为函数运算，并且避免使用程序状态以及易变对象。其中，λ 演算是该语言最重要的基础。而且λ 演算的函数可以接受函数作为输入的参数和输出的返回值。

这里所提到的λ 演算是指什么？对于计算机专业的学生而言，这个名词多少听说过，在我大学期间简单了解过演算规则，没想到现在可以和函数式编程关联。

Lambda

lambda 演算是由 Alonzo Church 创造出来世界上最小的程序设计语言，没有数字、字符串和布尔类型，但是 lambda 演算可以表示出任何图灵机。

其是由最简单的三个元素组成：变量、函数、应用。

名称	语法	例子	解释
变量	< name >	$x$	一个名为 $x$ 的变量
函数	$\lambda$ < parameters >.< body >	$\lambda x.x$	一个形参为 $x$ ，主体为 $x$ 的函数
应用	< function >< variable or function >	$(\lambda x.x)a$	以实参 $a$ 调用函数 $\lambda x.x$

\begin{array}{c}f({\color{#537FE7} x} ,{\color{#537FE7} y} ) & = & x^2+y^2\\f(2,3) & = & 2^2+3^2\end{array}

蓝色的 ${\color{#537FE7} x,y}$ 表示变量 $x$ 与变量 $y$ ， $x^2+y^2$ 则是函数，整体称之为应用。将上面的函数转换成 lambda 表达式如下：

\begin{array}{c}{\color{#ef6262} \lambda} {\color{#537FE7} x} {\color{#ef6262} \lambda} {\color{#537FE7} y}.x^2+y^2\\({\color{#ef6262} \lambda} {\color{#537FE7} x} {\color{#ef6262} \lambda} {\color{#537FE7} y}.x^2+y^2)(2,3)\\=2^2+3^2=13\end{array}

这里的 ${\color{#ef6262} \lambda} {\color{#537FE7} x} {\color{#ef6262} \lambda} {\color{#537FE7} y}$ 中的 ${\color{#ef6262} \lambda}$ 没有任何的意义，只是表示一个标志。

在 λ 演算只有两条真正的法则： $\alpha$ -变换和 $\beta$ -归约。

Alpha-变换规则表达的是，被绑定变量的名称是不重要的，它是对变量的重命名操作。举例： $\lambda x.x$ 和 $\lambda y.y$ 是同一个函数。

Beta-归约规则是对应用的替换操作。对于 $(\lambda x.x+1)3$ 这样的一个应用表达式，可以将 $x$ 替换成 $3$ ，得到 $3+1$ ，最终得到 $4$ 。

对于 lambda 演算没有数字，字符串以及任何非函数的数据类型。在 lambda 演算中没有 Ture 或者 False，也没有 0 和 1 只有通过 lambda 函数来表示的真值和假值，这里不做过多的说明，在维基百科中有详细说明 lambda 演算的图灵完备性。

这里只想引入数字的概念，在 lambda 演算中当然也没有数字的概念，只有通过函数来抽象定义数字。对于数字有如下定义：

n=\lambda f.f^n

这里的 n 不是代表 n 次幂，这里类似于嵌套函数的嵌套层数，如：

\begin{array}{c}0=\lambda f\lambda x.x\\1=\lambda f\lambda x.fx\\2=\lambda f\lambda x.f(fx)\\3=\lambda f\lambda x.f(f(fx))\\...\end{array}

这里已经不是传统的数字，是叫做 Church 数来对数字进行编码。当然可以通过对于函数的演算实现“数字”的加减法。

\begin{array}{c}(\lambda x\lambda y.x+y)(5)\\ = (\lambda y.5+y)\end{array}

传入 $x=5$ ，返回一个新的函数，新的函数接收另一个参数 $y$ ，返回 $x+y$ 的结果，这样产生的上下文也就是闭包。

const fn = (x) => {
  return (y) => {
    return x + y;
  };
};

这里引入了箭头函数，const fn = x => y => x + y，表示为一个单纯的运算式，箭头函数也可以看成 lambda 函数，它也符合前面所提到的 Alpha-变换和 Beta-归约。前面提到的 Church 数，也可以用箭头函数来进行模拟：

const zero = (f) => (x) => x;
const one = (f) => (x) => f(x);
const two = (f) => (x) => f(f(x));
const three = (f) => (x) => f(f(f(x)));

因此为了表示函数累加的概念，引入两个函数：

const times = (n) => (f) =>
  new Array(n)
    .fill(f)
    .reduce((acc, f) => (x) => f(acc(x)));
const count = (x) => x + 1;
console.log(times(7)(count)(0));

把 lambda 演算中的 $f$ 和 $x$ 分别取 $count$ 和 $x$ ，带入后可以得到所定义的“数字”，因此无论是在数学中还是 JS 中。所表达的“数字”都是等价的，也从侧面说明 lambda 演算与具体语言的表述无关。

Features

Pure Function

函数式编程，顾名思义跟函数相关，在我第一次接触到函数这个概念，应该是在初中的数学课上的正比例函数以及反比例函数。取任意一个自变量 $x$ 时，都可以得到一个因变量 $y$ ，并且每次取相同的值 $x$ 时，永远都会得到相同的 $y$ ，即：同一个输入，同一个输出。但是在数学世界里的函数不能和编程世界里的函数画上全等号，因为在编程世界里的函数，可能会随着时间的变化或是宿主环境的变化，输出不同的内容，例如:

function getToday() {
  return new Date().getDate();
}

这种不确定性可能会导致我们所写的程序难以调试，数据的变化在出现问题时难以追溯，以及函数的返回结果不便于复用。因此，希望将 JS 函数进行数学化来保证函数的拥有干净的输出，也就是说在函数中只进行计算，不受外部干预也不干预外部内容，摆脱不确定性以及副作用的影响，这两点便是纯函数解决了的两个大问题。计算是确定性的行为，而副作用则充满了不确定性。作为程序员，我们在开发的过程中，不再需要去关注函数可能会造成的外部影响，只需要关注函数本身的运算逻辑。

在计算机科学中，函数副作用指当调用函数时，除了返回可能的函数值之外，还对主调用函数产生附加的影响。 ——维基百科

这里也引出了函数式编程的前提，纯函数。在纯函数中，不需要考虑外部影响，只需要关注函数内部的运算逻辑，也就是说其是高度确定的函数。对于纯函数，其“纯”的本质在于显示数据流（函数除了入参和返回值之外，不以任何其它形式与外界进行数据交换）。

let name = "abc";
function foo() {
  return name;
}
foo();
name = "def";
foo();

现在来看纯函数作为函数式编程的特征，其并不是为了约束而约束，目的是为了追求更高的确定性以及提高代码的可靠性、可维护性和性能。第二个特征，函数是一等公民

First-Class Function

a programming language is said to have first-class functions if it treats functions as first-class citizens. ——wikipedia

函数是一等公民，从学习 JS 开始一直被反复提起，因为在 JS 中函数可以当作变量一样使用，也就意味着函数可以作为其他函数的参数传递，也可以作为一个函数的返回值，或者可以赋值给一个变量。

function foo() {
  return "Hello World";
}
function bar(fn) {
  return fn();
}
bar(foo);

function foo(a) {
  return function (b) {
    return a + b;
  };
}
foo();

const foo = function () {
  return "Hello World";
};
foo();

其中作为函数参数传递，也就是 JS 异步编程中常见的回调函数，监听事件便是常见的回调函数。函数之所以能为所欲为，是因为 foo 不只是一个函数，还是一个对象，根据 JS 中原型的关系，foo.__proto__ === Function.prototype，foo 具备 Function 原型上的所有方法。

注：没有一种数据类型叫做 Function，数据类型只有 Number、String、Boolean、Symbol、Object、Null、Undefined、BigInt，而 Function 和 Date 等都是对象类型。

Immutable Data

在上面提到的数据类型中，除了 Object，其他的都是值类型；而对于 Object 则是引用类型，这两者区别在于保存值类型的变量是按值访问的，保存引用类型的变量是按引用访问的。对于值类型，当想要修改值时，本质上是创造出一个新的值，因此值类型的数据无法被修改，均是不可变数据；对于引用类型，本质上是存储引用的地址，修改值则是修改原有引用的值，在数据被创建后，随时修改数据的内容，这种创建后仍然可以被修改的数据，称其为“可变数据”。

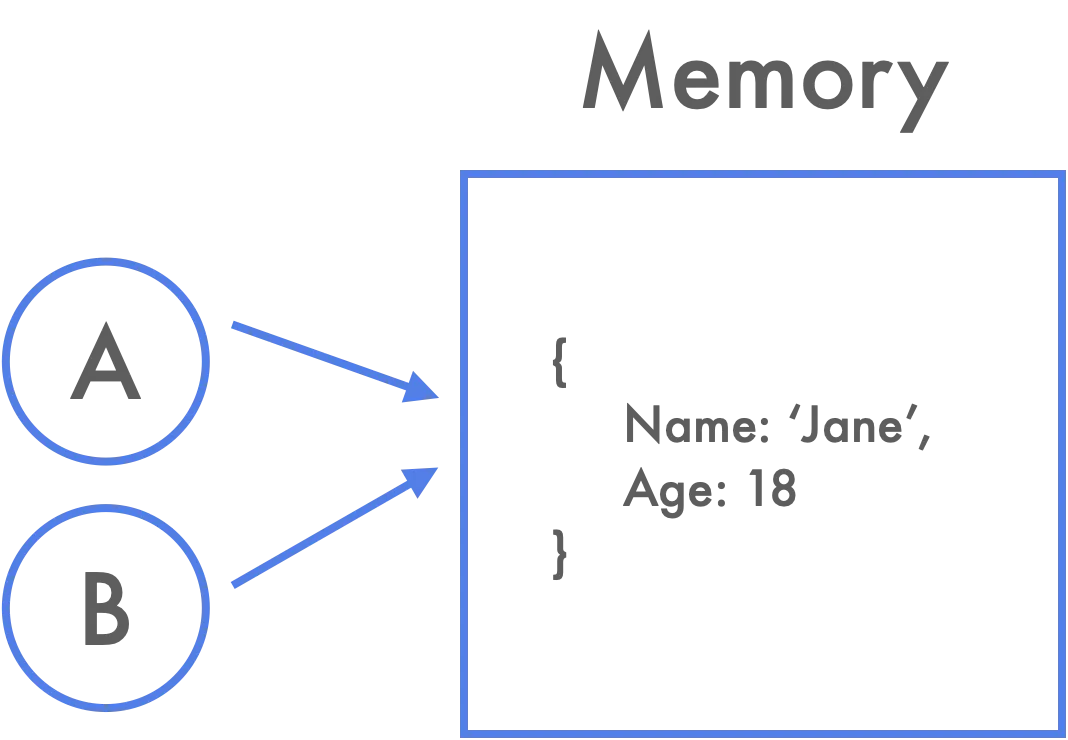
在引用类型中，常见的赋值操作，是把 a 的引用地址赋值给 b（也就是常说的浅拷贝），到了这里肯定会想到 ES6 引入的 const 关键字，对于引用类型 const 只能保证 a 不会被修改成其他引用类型的地址，并不能保证当前引用类型里字段或者数据的变化，const 只能保证值类型的数据不可变。

那么为什么函数式编程不喜欢可变数据呢？

function changeLevel(baseInfo, level) {
  const newInfo = baseInfo;
  newInfo.level = level;
  return newInfo;
}

可变数据带来的根本问题也是前面提到过的不确定性，会导致使用者甚至开发者自身都难以预测函数行为最终会指向什么结果；此外，函数的复用成本会增加，特别是当函数中存在可变数据时。在调用或复用函数之前，需要深入了解其逻辑细节，明确其对外部数据的依赖和影响情况，以确保调用动作的安全性。因此希望建立一个受控的黑盒，将变化控制在黑盒的内部，不去改变盒子外的任何东西，必须把可变数据从代码中剔除干净。对于上面 changeLevel 函数，常见的方法是利用深拷贝将 baseInfo 的值进行复制；虽然可以解决可变数据的问题，但是引出了新的问题：如果一个对象引用有上万个字段，或是对一些需要频繁更新数据又有高性能要求的场景（如：React），每次进行深拷贝都去遍历所有字段会消耗大量的内存，Facebook 在 2014 年推出 Immutable.js，接触过 React 的大多都知道这个库，而 Facebook 给它的定位“实现持久化数据结构的库”，先给一段样例代码体会下 Immutable.js 的强大。

const { Map } = require("immutable");

const map1 = Map({
  a: 1,
  b: 2,
  c: 3,
});

const map2 = map1.set({
  b: 50,
});

console.log("map1 === map2", map1 === map2);
// map1 === map2 false

Persistent Data Structure

可持久化：将数据结构的所有历史版本记录下来，称为可持久化。

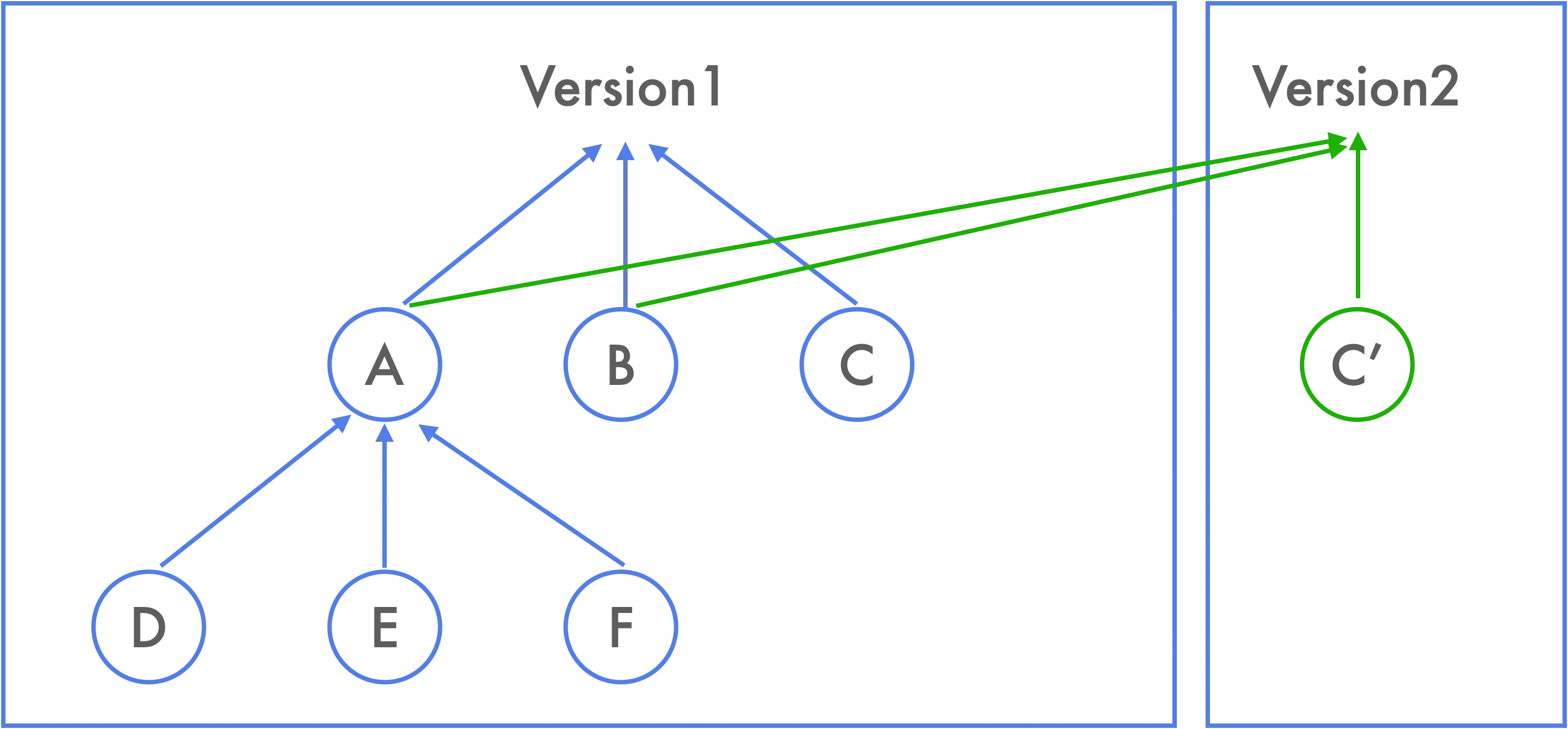
对于没接触过算法的前端开发者而言，可持续化数据结构可能会很陌生，但在我们开发中，git commit 的工作原理和它很相似。在 commit 发生时，git 会记录当前版本所有文件的索引，对于那些没有变化的文件，git 会保存他们原有的索引；对于那些以及发生变化的文件，git 会保存变化后的索引。如下图，当文件 C 发生变化变成 C’时，对于其他没有发生变化的文件，新的 commit 会直接指向它们的文件索引，并且会额外指向新的 C’。因此可以通过切换 commit 来查看不同版本的文件，着也是因为 commit 中记录了文件快照信息，这便是持久化数据结构的核心思想。这样再来看 Immutable.js 是如何实现基于 A 对象创建出了 B 对象就很好理解了。

const { Map } = require("immutable");

const A = Map({
  name: "Jane",
  hobby: "coding",
  age: 18,
  from: "China",
});

const B = A.set({
  name: "Tom",
});

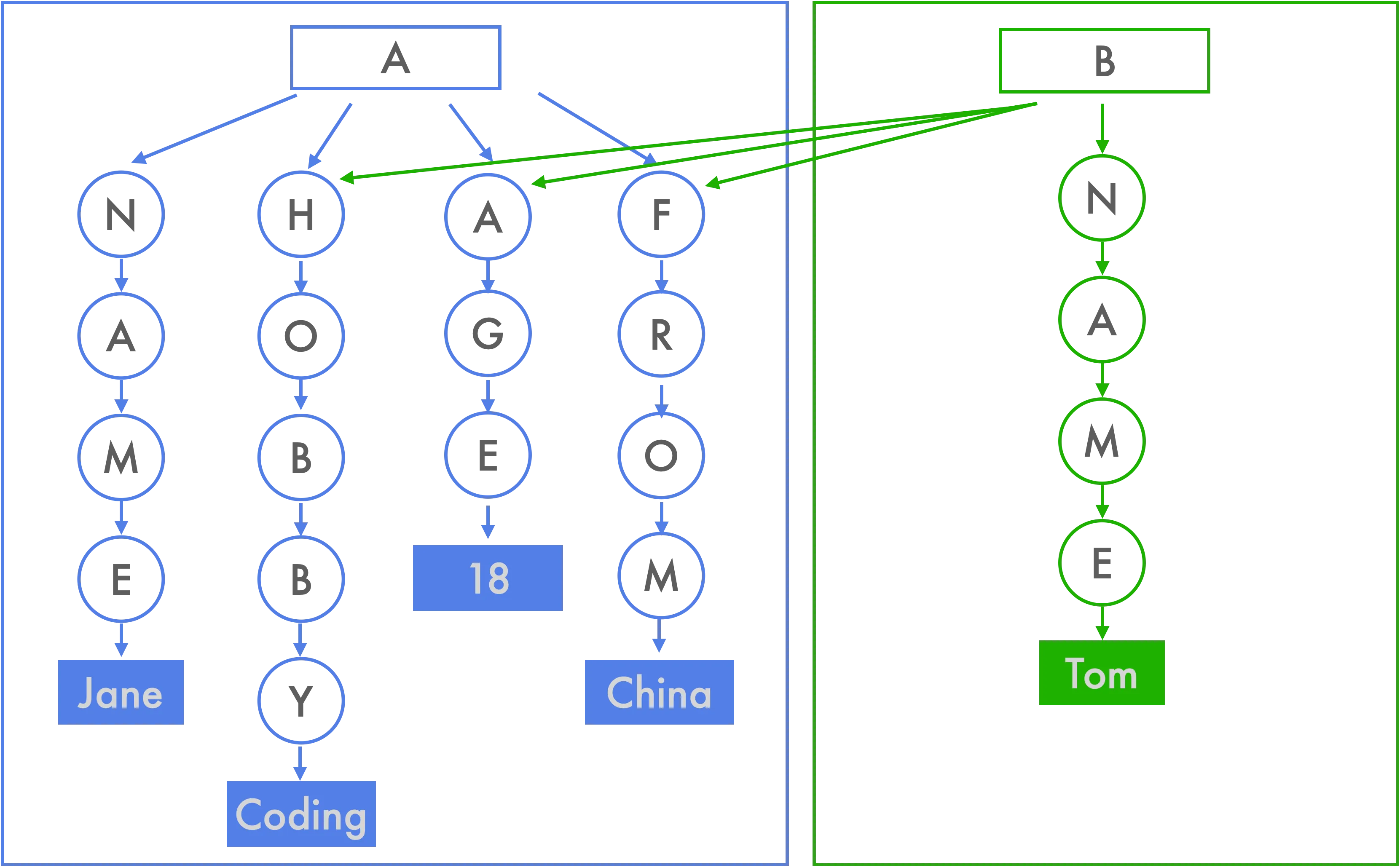
从上图来看，B 对象只需要指向新的 name 就完成了创建对象，达到“数据共享”的效果，持久化数据数据结构的底层依赖了另外的一种经典数据结构 Tire（字典树），对字典树的解释就不过多说明，主要是为了方便索引字段。

到此为止，简单了解了 Immutable.js 的工作原理以及 git 快照的索引管理，Immutable.js 的出现毫无疑问是持久化结构在前端领域影响最深远的一次实践。过去我以为算法在前端领域几乎没有太大的应用，但是现在看来，很多库、框架都离不开算法带来的优秀性能。

ImmerJS

可持久化数据结构并不是解决可变数据的唯一方法，在 ES6 中提出了 Proxy 代理拦截，2019 年 Immer.js 的发布，让不可变数据的解决方案，让开发者从 Immutable.js 迭代为了 Immer.js，因为不需要背 Immutable.js 定义的一大堆 API，只需要 import { produce } from "immer"，如下代码所示。

import { produce } from "immer";

const baseState = [
  {
    title: "Learn TypeScript",
    done: true,
  },
  {
    title: "Try Immer",
    done: false,
  },
];

const nextState = produce(baseState, (draft) => {
  draft[1].done = true;
  draft.push({ title: "Tweet about it" });
});

Immer.js 对 Proxy 的运用都蕴含在 produce 里。简化后的代码，如下所示，如果触发了 set 就会返回一个新的对象，“冻结”是为了避免意外的修改发生，保证数据的纯度。这里极简代码的函数拷贝可以进一步优化，完整的代码是可递归的，对于其他 Immer.js 的细节不做过多的理解，知道一些基本原理帮助理解即可（其他更多的细节，可以查看 Immer.js）。

function produce(base, recipe) {
  let copy;
  const draft = new Proxy(base, {
    set(obj, key, value) {
      if (!copy) {
        copy = { ...base };
      }
      copy[key] = value;
      return true;
    },
  });
  recipe(draft);
  return Object.freeze(copy || base);
}

目前社区提供了多种方法来解决可变数据的问题，其中 Immer.js 和 Immutable.js 是其中最出色的解决方案。Immutable.js 使用持久化数据结构作为底层实现，而 Immer.js 使用 Proxy 代理模式。尽管它们的具体工作原理不同，但它们的最终目的是相同的：确保数据引用和数据内容的变化能够同步发生，并在此过程中，根据需要处理具体的变化点，以提高不可变数据的执行效率。

Programming

在进入下一部分的学习之前，有必要明白一种软件设计原则，DRY(Don’t Repeat Yourself)，在编程时不要重复去做某一件事情，重复的内容抽成方法体，方便复用；而不是盲目的 ctrl+c，ctrl+v 重复赋值粘贴相同的代码。

HOF

HOF(Higher-Order Functions，高阶函数)在维基百科中的定义

在数学和计算机科学中，高阶函数是至少满足下列一个条件的函数:

接受一个或多个函数作为输入

输出一个函数

也就是接收函数作为入参，或者将函数作为出参返回的函数。对于高阶函数而言具体的好处可以从这个例子中体现出来。在开发过程中经常会遇到一种场景，判断当前 value 的数据类型；通常思路是定义一个 isType 函数，传入需要判断的数据类型和 value，如下代码。

function isType(type, value) {
  return (
    Object.prototype.toString.call(value) ===
    `[object ${type}]`
  );
}

isType("String", "a"); // true
isType("Number", "b"); // false
isType("String", 123); // false

实际上，如果我都判断 String 类型的话，函数的第一个参数都是一样的，可以进一步采用高阶函数进行优化，基于原有的 isType 方法进一步封装成 isString 判断是否属于字符串类型。

const isType = (type) => {
  return (value) =>
    Object.prototype.toString.call(value) ===
    `[object ${type}]`;
};
const isString = isType("String");
const isNumber = isType("Number");

isString("hello"); // isType('String')('hello')
isNumber(111); // isType('Number')(111)

现在来看封装思路，代码具有更好的可读性，以及更高的可复用性，后续的内容都建立在 HOC 基础之上。其实在开发中，有大量的方法都是采用了高阶函数的思想，例如最常用到的数组方法：reduce、map、filter、find 等等；其中 reduce 尤为特殊，不仅可以通过他推导出其他数组方法，更能推导出函数组合(也是函数式编程重要的思想，后续会提到)的过程。

Reduce

对于 reduce 不做过多解释，在 Array.prototype.reduce() 中详细提到了：

The reduce() method executes a user-supplied “reducer” callback function on each element of the array, in order, passing in the return value from the calculation on the preceding element. The final result of running the reducer across all elements of the array is a single value.

这里更加关注 reduce 的工作流执行过程，在思考 reduce 之前，先对 map 的工作流进行分析。

const arr = [1, 2, 3];
const newArr = arr.map((item) => item);
console.log(arr === newArr); // false
const addItemArr = arr.map((item) => item + 1); // [2,3,4];

从 arr === newArr 等于 false 易知 map 方法不会改变原有数组（不可变数据是函数式编程最基本的原则之一），newArr 是新创建出来的数组，符合对不可变数据的预期。

function map(arr, cb) => {
  const newArr = [];
  for (let i = 0; i < arr.length; i ++ ) {
    newArr.push(cb(arr[i]));
  }
  return newArr;
}

map 所表达的逻辑可以理解成上述代码，但 map 具体实现和上述代码大概率是不一样的。

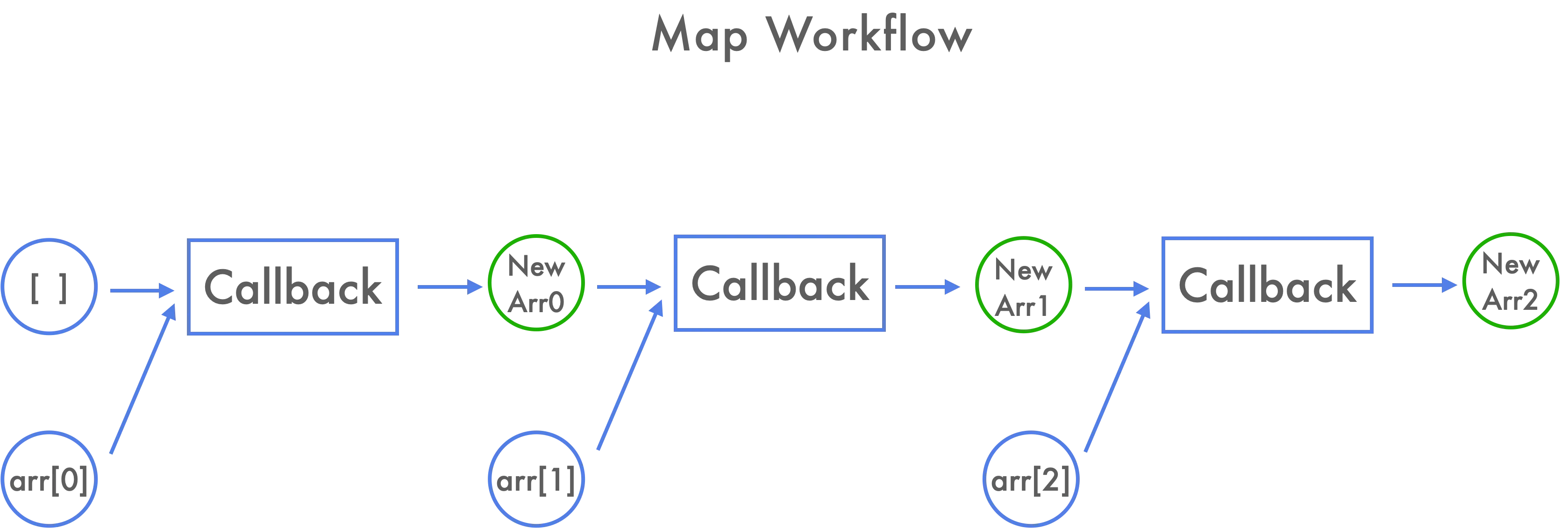
如图，在 map 的工作流中，数组的每一项都会带着上一次的结果去调用 callback，回调的结果一起流入下一个 callback；其实图中 map 的工作流和 reduce 非常相似，本质上就是 reduce 的一个过程。

const arr = [1, 2, 3];
const newArr = arr.reduce((pre, cur) => {
  pre.push(cur);
  return pre;
}, []);
console.log(arr === newArr); // false

map 只是相对于特殊的 reduce，map 回调后的结果只能是一个数组，而 reduce 回调函数和出参可以为任意值；了解了这些，可以知道 reduce 处在逻辑链相对底层的位置，也说明了其的重要性，但这只是对 reduce 有了一个初步认识，而 reduce 真正重要的是它对函数组合思想的映射。

通过 reduce 的工作流可以发现两个特征：reduce 过程构建了一个函数 pipe，回调函数在做参数组合。这两个特征不难理解，每次都是调用同一个回调，上一次的回调结果会作为下次回调的输入，但在 reduce 中每次的回调都是一样的，这点约束了 pipeline 的能力，因此可以想办法把 pipeline 里的每一个函数弄成不一样的。这里引用书中的了一个例子，考虑这样一个数字数组 arr：

const arr = [1, 2, 3, 4, 5, 6, 7, 8];

先需要将 arr 作为数据源，按照如下步骤指引一个求和操作：

筛选出 arr 里大于 2 的数字
将步骤 1 中筛选的数字乘以 2
对步骤 2 中的数组求和

const biggerThan2 = (num) => num > 2;
const multi2 = (num) => num * 2;
const add = (a, b) => a + b;

// step 1
const filteredArr = arr.filter(biggerThan2);
// step 2
const multipledArr = filteredArr.map(multi2);
// step 3
const sum = multipledArr.reduce(add, 0);

这里简单看下，只是需求 sum 这个值，中间的 filteredArr 和 multipledArr 完全是冗余常量，降低了代码的可读性，其次 filteredArr 和 multipledArr 作为引用类型，运行过程中可能会被修改，因此这段代码不简洁且不安全。这里可以借助数组方法进行链式调用，避免中间态和不安全的行为。

const sum = arr
  .filter(biggerThan2)
  .map(multi2)
  .reduce(add, 0);

但链式调用不是通用的方法，这些数组方法都是挂载在 Array 的原型 Array.prototype 上的，计算结束后都会 return 一个新的 Array，这个新的 Array 也可以继续访问 Array.prototype 的方法，也就是说链式调用存在前提条件。对于那些没有挂载在对象上的函数，不能进行链式调用，如下代码：

const add4 = (num) => num + 4;
const multiply3 = (num) => num * 3;
const divide2 = (num) => num / 2;

此时为了避免代码的不简洁和不安全性，可以把函数的执行结果作为下一个函数的入参传入，以此类推。

const sum = add4(multiply3(divide2(num)));

但随着调用函数的增加，这种调用方式会嵌套的越来越深，出现回调地狱，因此可以想办法通过函数式的思想去解决这些调用的问题。

compose/pipe

有了 reduce 工作流的铺垫，对于函数组合（compose）显得不是那么困难，只需要把 reduce 过程的每一个单元修改成任意函数既可，其工作流示意图如下所示：

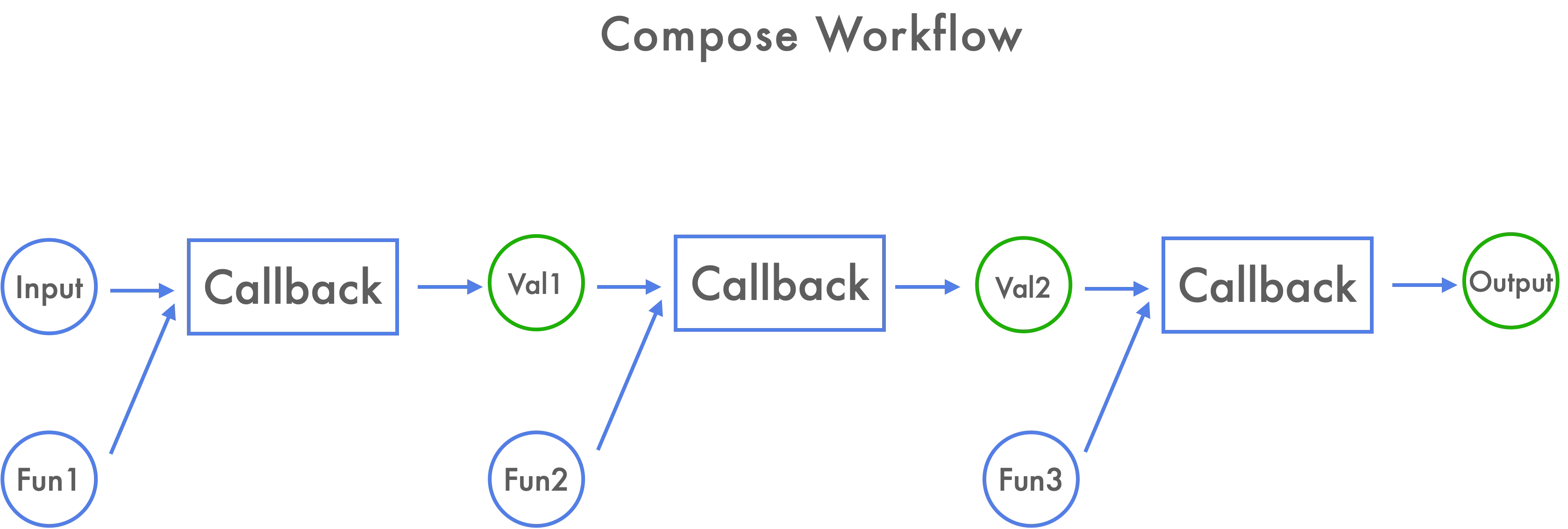
这些动态的函数来自于 reduce 的宿主数组，把当前工作流图片简化后代码如下所示，只需要在 callback 中依次调用函数计算上一个进来的值。

const funs = [func1, func2, func3];
funcs.reduce(callback, initalValue);

在 callback 中，有两个参数传入，上次计算结果和宿主数组传入的函数。callback(initalValue, func1) = func1(initalValue);

funcs.reduce((input, fn) => fn(input), 0);

这样可以借助 reduce 的工作流，完成不同函数的组合调用，进一步封装，可以得到 pipe。

const pipe = (...funcs) => {
  return (initalValue) => {
    return funcs.reduce(
      (input, fn) => fn(input),
      initalValue
    );
  };
};
const compute = pipe(add4, multiply3, divide2);
console.log(compute(10)); // 21

pipe 用于创建一个正序的函数执行顺序，而 compose 则是与 pipe 相反的，主要用于创建一个倒叙的函数执行顺序。只需要把上述代码的 reduce 换成 reduceRight 即可实现 compose 工作流。

对于为什么 pipe 是正序，compose 是倒序？这个问题会在范畴论中会了解到。

在过去面向对象的核心在于继承，而对于函数式编程而言，核心则在于组合。compose 组合多个函数的能力在函数式编程中是最具有代表性的工具函数。对于 compose 的实现，并不只有 reduce，还可以借助循环或是递归来完成，书中采用 reduce 来进行推导实现，主要是它的巧妙，把 reduce 和函数组合联系在一起。用循环解决的本质其实也是 reduce，这里我再用递归的思路实现下 pipe，如下代码：

const pipe = (...funcs) => {
  const cb = (param) => {
    const fn = funcs.shift();
    if (!fn) return param;
    return cb(fn(param));
  };
  return cb;
};

对于上面用 reduce 推导出的 pipe，其实有一个很大的缺陷，add4、multiply3、divide2 这一系列的函数是一元函数，属于是非常理想的情况下，如果把其中任意一个一元函数换成二元函数，最后的结果都会是 NaN；因此需要想办法解决参数对齐问题，需要对参数进行改造时，必然离不开函数式编程中另外两个重要的概念：偏函数和柯里化。

Currying

在没有系统学习函数式编程时，提到函数式编程一般就会想到柯里化，但本质上很少把柯里化单独使用起来，柯里化主要是把一个 N 元函数改造成 N 个相互嵌套的一元函数。如下代码：

function addThreeNum(a, b, c) {
  return a + b + c;
}

function addThreeNum(a) {
  return function (b) {
    return function (c) {
      return a + b + c;
    };
  };
}

另外偏函数和柯里化相似，只不过偏函数是将一个 N 元函数改造成一个 M 元函数（N < M）。在前面所提到偏函数求解组合链参数不对齐的问题，可以采用偏函数来解决。

const multiply = (x, y) => x * y;

const wrapFunc = (func, fixedParam) => {
  return (input) => {
    return func(fixedParam, input);
  };
};

const multiply4 = wrapFunc(multiply, 4);

这里仍然使用了高阶函数的思路，对现有的函数进行封装；因此在函数式编程思想中，面对一个有着多参的函数可以借助偏函数的思想避免重复的参数。这里虽然能前面解决参数不齐的问题，但随着参数增多，如果期望降到一元也很繁琐，因此可以借助柯里化来进一步解决问题。上面给了一个柯里化代码的例子，属于暴力枚举需要柯里化函数的参数，显然背离了函数式思想，因此最为重的是实现通用柯里化函数。通过分析柯里化函数执行流程，大致为：先得到函数参数个数，有多少参数嵌套多少层函数，嵌套的最后一层回调所有入参。因此这里用递归是最方便的实现方式：

const curry = (func) => {
  const argsLen = func.length;
  const generateCurried = (prevArgs) => {
    return (nextArg) => {
      const args = [...prevArgs, nextArg];
      if (args.length >= argsLen) {
        return func(...args);
      } else {
        return generateCurried(args);
      }
    };
  };
  return generateCurried([]);
};

这里用柯里化来处理组合链参数不齐的问题，将一系列参数不相同的函数进行柯里化后组合。

const add = (a, b) => a + b;
const quaternionMultiply = (a, b, c, d) =>
  a * b * c * d;
const divide = (a, b) => a / b;

const curriedAdd = curry(add);
const curriedMultiply = curry(quaternionMultiply);
const curriedDivide = curry(divide);

const compute = pipe(
  curriedAdd(1),
  curriedMultiply(2)(3)(4),
  curriedDivide(144)
);

console.log(compute(2)); // 2

在很多常见下，通常会使用这类范式进行编程，类似于进行数学推导或类型推导。它使我们能够像学习数学一样，将复杂的问题简化，并通过逐步累加或累积的方式得出结果。至此，函数式编程中常见的思维原则已经有了初步的认识，后续会结合范畴论的知识对函数式编程进一步深入学习理解。最后想说下，在数学世界里，我们常常定义函数是集合 A 到集合 B 的一种映射；在函数式编程中，函数也是类似，只不过是将数据从某种形态“映射（态射）”到另一种形态，这点会在范畴论中体现。

Functional Programming